Στο παράδειγμα αυτό , θα αναλύσουμε τιμές θερμοκρασίας. Τα δεδομένα μας, είναι οι μέσες ετήσιες Τιμές θερμοκρασίας τού αέρα στην περιοχή του αεροδρομίου της Θεσσαλονίκης.  Θα υπολογίσουμε τη μέση θερμοκρασία της περιόδου 1947 - 1988 και την ευθεία ελαχίστων τετραγώνων για να βρούμε την τάση τής θερμοκρασίας.

Εισάγουμε τα δεδομένα τού παραπάνω πίνακα στην περιοχή Α1:Β42. Τα έτη θα βρίσκονται στην περιοχή Α1:Α42 και οι μέσες ετήσιες θερμοκρασίες στην περιοχή Β1:Β42. Το φύλλο εργασίας μας, πρέπει να μοιάζει μ' αυτό της παρακάτω οθόνης.

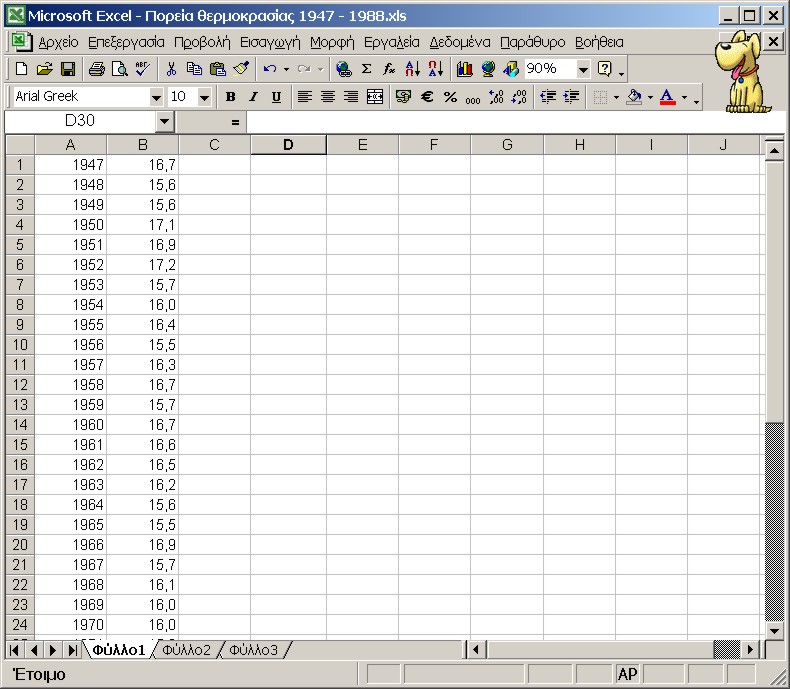
Η μέση ετήσια τιμή τής θερμοκρασίας για την περίοδο 1947 - 1988, καθώς και η μέγιστη και ελάχιστη τιμή της, υπολογίζονται εύκολα με Τις συναρτήσεις AVERAGE, ΜΑΧ και ΜΙΝ. Στα κελιά Ε1, Ε2 και Ε3 εισάγουμε αντίστοιχα τους τύπους =ΜΑΧ(Β1 : Β42), =ΑVERAGE(B1 :Β42) και =ΜΙΝ(Β1 : Β42).

Στο κελί Ε6 εισάγουμε τον τύπο =STDEV(B1:B42) για να βρούμε την τυπική απόκλιση των τιμών.
Τα αποτελέσματα των τύπων φαίνονται στην παρακάτω οθόνη:

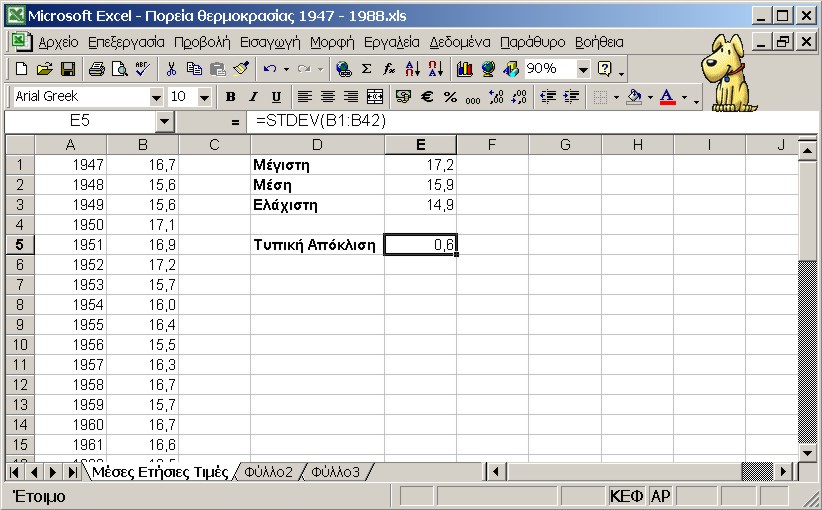
Από τα παραπάνω αποτελέσματα συμπεραίνουμε, ότι τα 42 αυτά χρόνια οι ετήσιες Τιμές κυμάνθηκαν κατά 2,3°C.

Η τιμή της τυπικής απόκλισης (± 0,6) βεβαιώνει τη μικρή πράγματι διασπορά των τιμών αυτών.

Για να βρούμε την κατανομή αποκλίσεων των μέσων ετήσιων τιμών, θα χρησιμοποιήσουμε τη συνάρτηση FREQUENCY. Η συνάρτηση αυτή υπολογίζει τη συχνότητα εμφάνισης τιμών μέσα σε κάποια διαστήματα (κλάσεις) και την αποδίδει σαν κατακόρυφο πίνακα. .
Ένας δεύτερος τρόπος για να βρούμε τη συχνότητα εμφάνισης τιμών είναι το εργαλείο ανάλυσης Ιστόγραμμα. Το εργαλείο αυτό, μας δίνει επίσης τη δυνατότητα να δημιουργήσουμε ένα ενσωματωμένο ιστόγραμμα.

Ενδιαφέρον για μας, έχει το πλήθος των τιμών μεταξύ m ± σ και m ± 2σ (όπου m η μέση ετήσια υιμή της θερμοκρασίας και σ η τυπική απόκλιση).

Για να ορίσουμε τα διαστήματα αυτά, εισάγουμε στα κελιά D8:D12 τους τύπους =Ε2-2*Ε5, =Ε2-Ε5, =Ε2, =Ε2+Ε5 και =Ε2+2*Ε5. Επειδή η συνάρτηση επιστρέφει μία Τιμή περισσότερη από τα στοιχεία του πίνακα των διαστημάτων, επιλέγουμε την περιοχή E8:D13. Στο κελί Ε8 εισάγουμε τον τύπο =FREQUENCY(D8:D12;E8:E13) και πατάμε το συνδυασμό πλήκτρων [Ctri]+[Shift]+ [Enter].

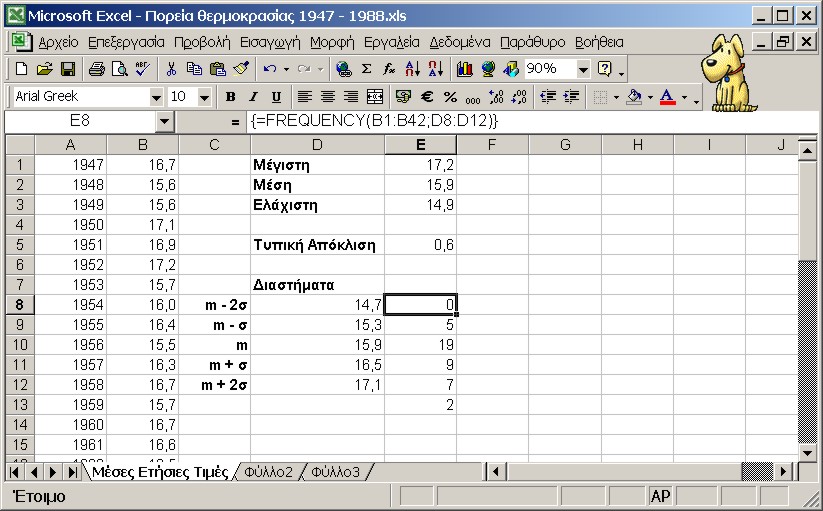
Σύμφωνα με τα παραπάνω αποτελέσματα, 28 Τιμές (το 66%) βρίσκονται μεταξύ των ορίων m ±σ, ενώ 42 Τιμές (95%) μεταξύ των ορίων m ±2σ.

Για να βρούμε τη γραμμή τάσης, θα χρησιμοποιήσουμε τη συνάρτηση LINEST. Η συνάρτηση αυτή χρησιμοποιεί τη μέθοδο των ελαχίστων τετραγώνων, για να υπολογίσει την ευθεία που περιγράφει με το βέλτιστο τρόπο τα δεδομένα μας. Η εξίσωση της ευθείας ελαχίστων τετραγώνων είναι:

y = ax+ b

όπου x είναι η ανεξάρτητη μεταβλητή, y η εξαρτημένη μεταβλητή, a η κλίση της ευθείας και b το σημείο στο οποίο η ευθεία τέμνει τον άξονα των y.
Επειδή η συνάρτηση αποδίδει έναν πίνακα τιμών, πρέπει να καταχωρισθεί σαν τύπος πίνακα. Επιλέγουμε τα κελιά G2 και Η2 και πληκτρολογούμε τον τύπο =LINEST(B1 :Β42). Πατάμε το συνδυασμό πλήκτρων [Ctrl]+[Shift]+ [Enter] για να εισαγάγουμε τον τύπο.

Σύμφωνα με τα παραπάνω αποτελέσματα, ότι η γραμμή τάσης έχει μαθηματικό πρότυπο:

y =  16,486 – 0,028 * x

Για να υπολογίσουμε τα σημεία τής ευθείας αυτής, εισάγουμε στο κελί Ι1 την τιμή 16,486 και στο κελί Ι2 τον τύπο =Ι1- 0,028. Αντιγράφουμε τον τύπο σύροντας τη λαβή συμπλήρωσης ως το κελί Ι42. Οι τιμές αυτές αποτελούν τις τεταγμένες τής ευθείας ελαχίστων τετραγώνων.

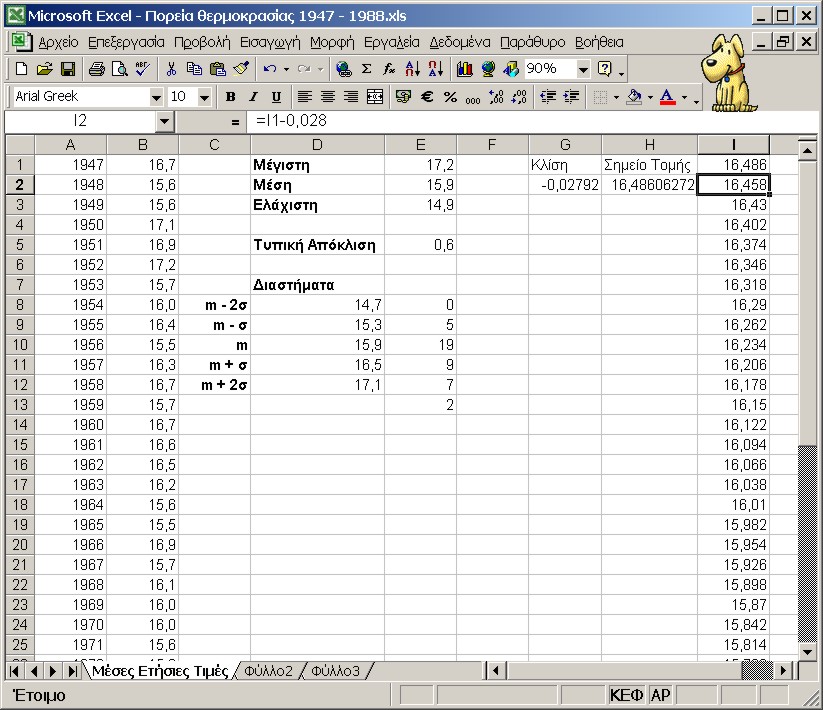
Για να δημιουργήσουμε το γράφημα με την πορεία της θερμοκρασίας, κάνουμε κλικ στο κουμπί οδηγός γραφημάτων της βασικής γραμμής εργαλείων. Επιλέγουμε σαν τύπο γραφήματος (Διασπορά) ΧΥ και για δευτερεύοντα τύπο γραφήματος Διασπορά με σημεία δεδομένων που συνδέονται με ομαλές γραμμές χωρίς δείκτες.

Στο επόμενο παράθυρο διαλόγου εισάγουμε τις περιοχές των δεδομένων μας. Επιλέγουμε με το ποντίκι την περιοχή Α1:Β42 και την περιοχή Ι1:Ι42 (με [Ctrl] και κλικ).

Στο παράθυρο διαλόγου "Οδηγός γραφημάτων - Επιλογές γραφήματος" πληκτρολογούμε σαν τίτλο γραφήματος Πορεία θερμοκρασίας 1947-1988 και ^οC για ετικέτα τού άξονα τιμών Υ.

Στο τελευταίο παράθυρο διαλόγου κάνουμε κλικ στο κουμπί Τέλος, για να εισαγάγουμε το γράφημα σαν αντικείμενο στο φύλλο εργασίας.
Με μερικές μορφοποιήσεις το γράφημα παίρνει την παρακάτω μορφή:

Ο κινητός μέσος όρος (κυλιόμενος μέσος) εξομαλύνει τις διακυμάνσεις των δεδομένων, επισημαίνοντας έτσι καλύτερα την τάση τους.

Για να προσθέσουμε τον κινητό μέσο όρο στο γράφημα, ακολουθούμε τα παρακάτω βήματα:

• Επιλέγουμε το γράφημα και κάνουμε κλικ στη σειρά δεδομένων, στην οποία θέλουμε να προσθέσουμε κινητό μέσο όρο.
• Στο μενού Γράφημα, επιλέγουμε τη διαταγή Προσθήκη γραμμής τάσης.
• Εμφανίζεται το ομώνυμο παράθυρο διαλόγου, στην καρτέλα Τύπος του οποίου επιλέγουμε σαν τύπο τάσης "Κυλιόμενος μέσος".

• Στο πλαίσιο "Περίοδος" εισάγουμε το πλήθος των περιόδων που θα χρησιμοποιηθούν για τον υπολογισμό του κινητού μέσου όρου.
• Κάνουμε κλικ στο κουμπί ΟΚ.