1 x 1, 1 x 1,1 x 1,1 x 1,1 x 1,1

που δίνει αποτέλεσμα 1,61€.
Για να υπολογίσουμε τη σημερινή αξία ενός ευρώ που θα λάβουμε μετά από 5 χρόνια με την ίδια απόδοση, εκτελούμε τον αντίστροφο υπολογισμό

1 / 1,1 / 1,1 / 1,1 / 1,1 / 1,1

που δίνει αποτέλεσμα 0,62€.

Στο παρακάτω παράδειγμα, θα υπολογίσουμε την απόδοση μιας επένδυσης, γνωρίζοντας εκ των προτέρων τις καθαρές εισροές χρημάτων κάθε χρονιάς.  Έστω ότι επενδύουμε το ποσό των 20.000,00€ και οι καθαρές εισροές χρημάτων για τα επόμενα χρόνια είναι 3, 5 , 7 και 15 χιλιάδες ευρώ.  Δημιουργούμε το παρακάτω φύλλο εργασίας, όπου στο κελί C4 εισάγουμε τον τύπο =B4+C2 και σύροντας τη λαβή συμπλήρωσης μέχρι το κελί F4, βρίσκουμε τη συσσωρευμένη εισροή χρημάτων κάθε χρονιάς.

Στο κελί Β6 εισάγουμε το ετήσιο ποσοστό επιτοκίου (υποτίθεται σταθερό 10% για όλο το χρονικό διάστημα). Για τον υπολογισμό τού συντελεστή, εισάγουμε στο κελί Β8 τον τύπο =1/(1+$Β$6)^Β1 και σύροντας τη λαβή συμπλήρωσης μέχρι το κελί F8.

Γενικά, για τον υπολογισμό τής παρούσας και μελλοντικής αξίας, χρησιμοποιούμε τον τύπο 1/(1+χ)^ν, όπου ν ο αριθμός τής περιόδου και χ το επιτόκιο. Αν το επιτόκιο είναι κυμαινόμενο, ο τύπος παίρνει τη μορφή 1/(1+x)¹ + 1/(1+y)² + 1/(1+z)³ + ... όπου x, y, z  τα επιτόκια κάθε περιόδου.

Πληκτρολογούμε στο κελί Β10 τον τύπο =Β2*Β8 και σύροντας τη λαβή συμπλήρωσης μέχρι το κελί F10, το φύλλο εργασίας παίρνει την παρακάτω μορφή:

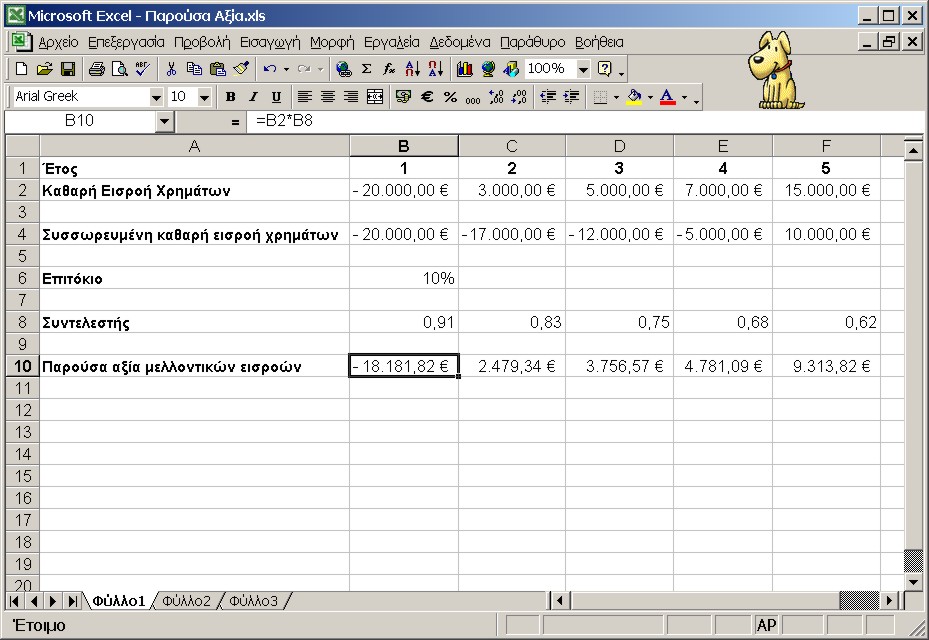
Οι συντελεστές 0,91 στο τέλος τού πρώτου χρόνου έως και 0,62 στο τέλος του πέμπτου χρόνου, αντιπροσωπεύουν την αξία ενός σημερινού ευρώ ύστερα από ένα έως πέντε χρόνια. Πολλαπλασιάζουμε τις καθαρές εισροές κάθε έτους με τον αντίστοιχο συντελεστή και παίρνουμε τις μελλοντικές εισροές χρημάτων κάθε χρονιάς, με βάση την παρούσα αξία τους. Σύμφωνα με τα παραπάνω, η επένδυση θα αποδώσει ύστερα από 5 χρόνια 9.313,82€ σημερινής αξίας.